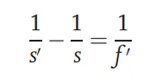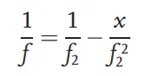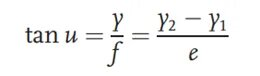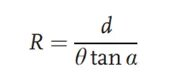Optik Sistemlerin Odak Uzaklığı Tanımı ve Test Yöntemleri

1.Optik Sistemlerin Odak Uzaklığı

Odak uzaklığı optik sistemin çok önemli bir göstergesidir, odak uzaklığı kavramını az çok anlamışızdır, burada inceleyeceğiz.
Bir optik sistemin odak uzaklığı, paralel ışık düştüğünde optik sistemin optik merkezinden ışının odağına olan mesafe olarak tanımlanır ve optik sistemdeki ışığın konsantrasyonunun veya diverjansının bir ölçüsüdür. Bu kavramı göstermek için aşağıdaki diyagramı kullanırız.

Yukarıdaki şekilde, sol uçtan gelen paralel ışın, optik sistemden geçtikten sonra görüntü odağı F'ye yakınsar, yakınsayan ışının ters uzantı çizgisi, gelen paralel ışının karşılık gelen uzantı çizgisiyle bir noktada kesişir ve bu noktadan geçen ve optik eksene dik olan yüzeye arka ana düzlem denir, arka ana düzlem optik eksenle P2 noktasında kesişir, buna ana nokta (veya optik merkez noktası) denir, ana nokta ile görüntü odağı arasındaki mesafeye genellikle odak uzaklığı denir, tam adı görüntünün etkin odak uzaklığıdır.
Şekilden ayrıca optik sistemin son yüzeyinden görüntünün odak noktası F'ye kadar olan mesafeye arka odak uzaklığı (BFL) denildiği görülebilir. Buna uygun olarak, paralel ışın sağ taraftan geliyorsa, etkili odak uzaklığı ve ön odak uzaklığı (FFL) kavramları da vardır.

2. Odak Uzaklığı Test Yöntemleri

Pratikte, optik sistemlerin odak uzaklığını test etmek için kullanılabilecek birçok yöntem vardır. Farklı prensiplere dayanarak, odak uzaklığı test yöntemleri üç kategoriye ayrılabilir. İlk kategori görüntü düzleminin konumuna dayanır, ikinci kategori odak uzaklığı değerini elde etmek için büyütme ve odak uzaklığı arasındaki ilişkiyi kullanır ve üçüncü kategori odak uzaklığı değerini elde etmek için birleşen ışık huzmesinin dalga cephesi eğriliğini kullanır.
Bu bölümde optik sistemlerin odak uzaklığını test etmek için yaygın olarak kullanılan yöntemleri tanıtacağız:：

2.1Collimator Yöntemi

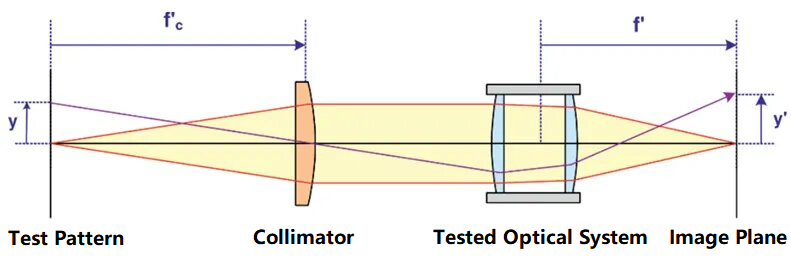
Bir optik sistemin odak uzaklığını test etmek için bir kolimatör kullanmanın prensibi aşağıdaki şemada gösterildiği gibidir:

Şekilde, test deseni kolimatörün odak noktasına yerleştirilmiştir. Test deseninin yüksekliği y ve odak uzaklığı f_c' kolimatörün bilinmektedir. Kolimatör tarafından yayılan paralel ışın test edilen optik sistem tarafından birleştirildikten ve görüntü düzleminde görüntülendikten sonra, optik sistemin odak uzaklığı görüntü düzlemindeki test deseninin y' yüksekliğine göre hesaplanabilir. Test edilen optik sistemin odak uzaklığı aşağıdaki formülü kullanabilir:

2.2 GaussMyöntem
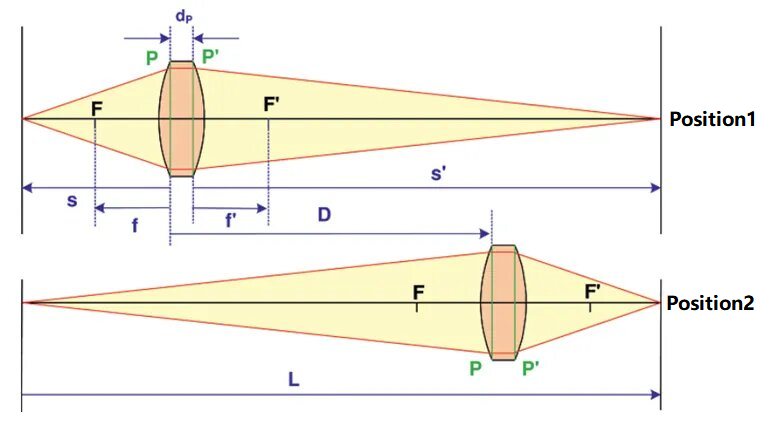
Bir optik sistemin odak uzaklığını test etmek için Gauss yönteminin şematik şekli aşağıda gösterilmiştir:

Şekilde, test edilen optik sistemin ön ve arka ana düzlemleri sırasıyla P ve P' ile gösterilmektedir ve iki ana düzlem arasındaki mesafe d'dir._PBu yöntemde d değeri_Pbilinen olarak kabul edilir veya değeri küçük ve göz ardı edilebilir. Bir nesne ve bir alıcı ekran sol ve sağ uçlara yerleştirilir ve aralarındaki mesafe L olarak kaydedilir, burada L'nin test edilen sistemin odak uzunluğunun 4 katından büyük olması gerekir. Test edilen sistem sırasıyla konum 1 ve konum 2 olarak gösterilen iki konuma yerleştirilebilir. Soldaki nesne alıcı ekranda açıkça görüntülenebilir. Bu iki konum arasındaki mesafe (D olarak gösterilir) ölçülebilir. Eşlenik ilişkiye göre şunları elde edebiliriz:

Bu iki konumda, nesne uzaklıkları sırasıyla s1 ve s2 olarak kaydedilir, böylece s2 - s1 = D olur. Formül türetme yoluyla, optik sistemin odak uzaklığını aşağıdaki gibi elde edebiliriz:

2.3Lensometre
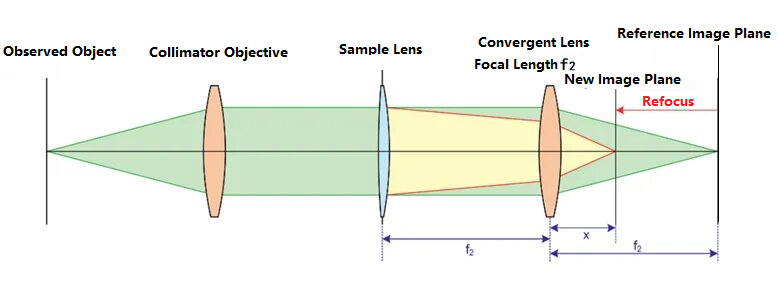
Lensometre uzun odak uzaklıklı optik sistemleri test etmek için oldukça uygundur. Şematik şekli aşağıdaki gibidir:

İlk olarak, test edilen lens optik yola yerleştirilmez. Soldaki gözlenen hedef kolimatör lensten geçer ve paralel ışık haline gelir. Paralel ışık, f odak uzaklığına sahip bir yakınsak lens tarafından yakınlaştırılır.₂ve referans görüntü düzleminde net bir görüntü oluşturur. Optik yol kalibre edildikten sonra, test edilen lens optik yola yerleştirilir ve test edilen lens ile yakınsak lens arasındaki mesafe f₂Sonuç olarak, test edilen merceğin eylemi nedeniyle ışık huzmesi yeniden odaklanacak ve görüntü düzleminin konumunda bir kaymaya neden olacak ve diyagramdaki yeni görüntü düzleminin konumunda net bir görüntü elde edilecektir. Yeni görüntü düzlemi ile yakınsak mercek arasındaki mesafe x olarak gösterilir. Nesne-görüntü ilişkisine dayanarak, test edilen merceğin odak uzaklığı şu şekilde çıkarılabilir:

Uygulamada lensometre, gözlük camlarının üst odak ölçümünde yaygın olarak kullanılmaktadır ve basit kullanım ve güvenilir hassasiyet avantajlarına sahiptir.

2.4 RahipRefraktometre

Abbe refraktometresi optik sistemlerin odak uzaklığını test etmek için başka bir yöntemdir. Şematik şekli aşağıdaki gibidir:

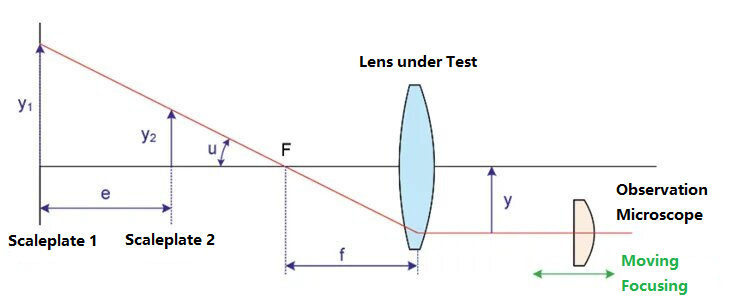
Test edilen merceğin nesne yüzey tarafına farklı yüksekliklerde iki cetvel yerleştirin, yani ölçek plakası 1 ve ölçek plakası 2. Karşılık gelen ölçek plakalarının yükseklikleri y1 ve y2'dir. İki ölçek plakası arasındaki mesafe e'dir ve cetvelin üst çizgisi ile optik eksen arasındaki açı u'dur. Ölçek plakası, f odak uzaklığına sahip test edilen mercek tarafından görüntülenir. Görüntü yüzeyi ucuna bir mikroskop yerleştirilir. Mikroskobun konumunu hareket ettirerek, iki ölçek plakasının üst görüntüleri bulunur. Bu sırada, mikroskop ile optik eksen arasındaki mesafe y olarak gösterilir. Nesne-görüntü ilişkisine göre, odak uzaklığını şu şekilde elde edebiliriz:

2.5 Moire Sapma ÖlçümüYöntem
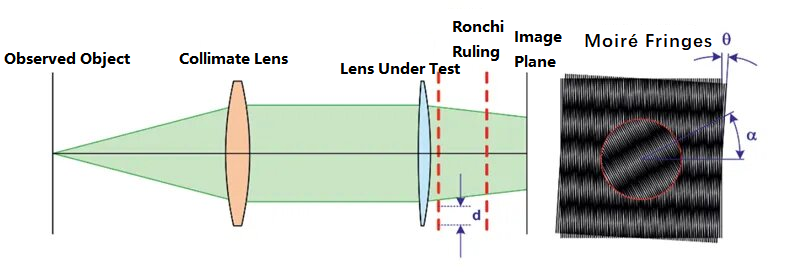
Moiré deflektometri yöntemi, paralel ışık huzmelerinde iki set Ronchi kuralı kullanacaktır. Ronchi kuralı, optik sistemlerin performansını test etmek için yaygın olarak kullanılan, cam bir alt tabaka üzerine biriktirilmiş metal krom filminin ızgara benzeri bir desenidir. Yöntem, optik sistemin odak uzaklığını test etmek için iki kafes tarafından oluşturulan Moiré saçaklarındaki değişimi kullanır. İlkenin şematik diyagramı aşağıdaki gibidir:

Yukarıdaki şekilde, gözlenen nesne kolimatörden geçtikten sonra paralel bir ışın haline gelir. Optik yolda, önce test edilen lens eklenmeden, paralel ışın θ yer değiştirme açısına ve d ızgara aralığına sahip iki ızgaradan geçerek görüntü düzleminde bir dizi Moiré saçakları oluşturur. Daha sonra, test edilen lens optik yola yerleştirilir. Orijinal kolime edilmiş ışık, lens tarafından kırıldıktan sonra belirli bir odak uzaklığı üretecektir. Işık huzmesinin eğrilik yarıçapı aşağıdaki formülden elde edilebilir:

Genellikle test edilen lens ilk ızgaraya çok yakın yerleştirilir, bu nedenle yukarıdaki formüldeki R değeri lensin odak uzunluğuna karşılık gelir. Bu yöntemin avantajı, pozitif ve negatif odak uzunluklu sistemlerin odak uzunluğunu test edebilmesidir.

2.6 OptikFiberAotokollimasyonMyöntem
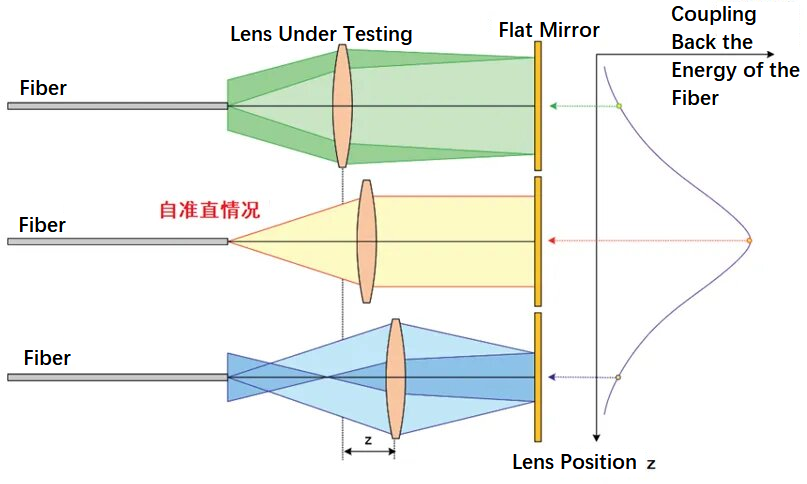
Aşağıdaki şekilde, lensin odak uzaklığını test etmek için optik fiber otokolimasyon yönteminin kullanılması ilkesi gösterilmektedir. Test edilen lensin içinden geçen ve ardından bir düzlem aynaya ulaşan ıraksak bir ışın yaymak için fiber optik kullanır. Şekildeki üç optik yol, optik fiberin sırasıyla odak içindeki, odak içindeki ve odak dışındaki koşullarını temsil eder. Test edilen lensin konumunu ileri geri hareket ettirerek, fiber kafasının odaktaki konumunu bulabilirsiniz. Bu sırada, ışın kendi kendine kolime olur ve düzlem ayna tarafından yansıtıldıktan sonra enerjinin çoğu fiber kafasının konumuna geri döner. Yöntem prensip olarak basittir ve uygulanması kolaydır.

3.Sonuç

Odak uzaklığı, bir optik sistemin önemli bir parametresidir. Bu makalede, optik sistem odak uzaklığı kavramını ve test yöntemlerini ayrıntılı olarak açıklıyoruz. Şematik diyagramla birlikte, görüntü tarafı odak uzaklığı, nesne tarafı odak uzaklığı ve ön-arka odak uzaklığı kavramları dahil olmak üzere odak uzaklığının tanımını açıklıyoruz. Uygulamada, bir optik sistemin odak uzaklığını test etmek için birçok yöntem vardır. Bu makalede, kolimatör yöntemi, Gauss yöntemi, odak uzaklığı ölçüm yöntemi, Abbe odak uzaklığı ölçüm yöntemi, Moiré sapma yöntemi ve optik fiber otokolimasyon yönteminin test prensipleri tanıtılmaktadır. Bu makaleyi okuyarak optik sistemlerdeki odak uzaklığı parametrelerini daha iyi anlayacağınıza inanıyorum.